Student: Ashley Peternella
Supervisor: Dr. Jean Derks
Semester: 2015-2016
Problem statement and motivation:
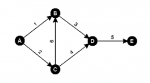
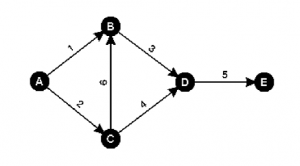
Project managers are charged with the responsibility of managing all the tasks within a project to ensure that the project is completed within an agreed deadline, with a certain quality, and for an agreed price. To know how much attention they need to invest in each task, managers need a measure that can capture the feature of ‘criticality’ of the tasks of a specified project. Criticality is defined as the importance of managing the duration of a task.
Changing a task’s link to test criticality based on dependency
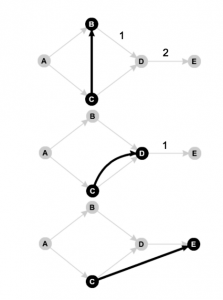
Inspired by the pessimistic bankruptcy game for the problem of cost sharing, this article explores the idea of using the combination of cooperative game theory and the Shapley value as a method for capturing the expected features of criticality.
Those features are: correlation between task duration and duration of the entire project, probability of being on ‘the critical path’, relation to other tasks, and task dependencies.
The research presented will show that pessimistic games in their purist forms only further formalise the concept of cruciality, which is the importance of managing the duration- uncertainty of tasks. An adapted method is created, which will be proven to capture the desired features of criticality, and serve as proof of concept.
Research hypothesis:
Cooperative game theory could help define the feature of criticality of tasks within project management.
Major outcome:
The adapted method seems to capture all desired features of criticality and thus serves as proof of concept.
References:
- Branzei, R., Ferrari, G., Fragnelli, V., and Tijs, S. (2002). Two approaches to the problem of sharing delay costs in joint projects. Annals of Operational Research, Vol. 109, pp. 359–374.
- Castro, J., Daniel, G., and Tejada, J. (2007). A project game for PERT networks. Operations Research Letters 35, pp. 791–798.
- Elmaghraby, S.E. (2000). On criticality and sensitivity in activity networks. European Journal of Operational Research, Vol. 127, No. 2, pp. 220–238.
- Steiner, G.A. (1969). Top management planning macmillan. Quoted on page 481 of Project Management Handbook, 2nd edition.
- Williams, T. (2003). The contribution of mathematical modelling to the practice of project management. IMA J Management Math, Vol. 14, No. 1, pp. 3–30.
Download: Report