Fanorona
Fanorona is a board game with its roots in Madagascar. It is derived from the game “Alquerque”, which might be over 3000 years old. The goal of the game is to capture all opponent pieces. The game is a draw if neither player succeeds.
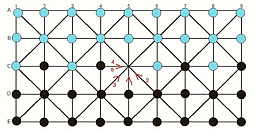
Fanorona has three standard versions: Fanoron-Telo, Fanoron-Dimyand, and Fanoron-Tsivy. The difference between these versions is the board size. Fanoron-Telo is played on a 3×3 board and the difficulty of this game can be compared to the game of Tic-Tac-Toe. Fanoron-Dimyand is played on a 5×5 board and Fanoron-Tsivy is played on a 5×9 board. Fanoron-Tsivy is usually called Fanorona, because it is the best-known board size. The Fanorona board consists of lines and intersections. A line represents the path along which a piece can move during the game. There are weak and strong intersections.
On a weak intersection it is only possible to move a piece horizontally and vertically, while on a strong intersection it is also possible to move a piece diagonally. A piece can only move from one intersection to an adjacent intersection. In the initial position each player has 22 pieces. Players move alternately; White move first.
Solving the game
Solving the game was done in two stages. The first stage
was constructing an endgame database. When analysizing the game we saw that most moves are played with
few pieces on the board. Thus endgame databases proved
to be quite successful for Fanorona. During the
research we managed to make a 7 piece endgame
database. This means that we solved all positions
with 7 or fewer pieces on the board and stored that
information in a file. It turned out that there exist
a total of 6,261,651,660 different positions with 7
or fewer pieces on the board and the database used 3.6
GB of hard disk space. The construction of the 4vs3
database alone took more then three weeks. In total
more then 2 months were used to compute all endgame
databases.
The second step was to implement a search technique
called “Proof-number search”. This technique stores the search tree in
memory and chooses the most promising node for
evaluation. Thus PN search (Proof-number search) is a
best first search. PN search uses for each node a
proof number and a disproof number to indicate how many nodes at least
have to be evaluated in order to prove the goal of
the search. The goal of the search can be to prove that “White
wins the game when playing optimally”.
The combination of the endgame database and the
customized PN form the core of the program
KINGRALOMBO. This program was able to solve the start
position of Fanorona in more than a week of computing
time. It turns out that the Fanorona is a draw.
130,820,097,938 nodes were created during the search
to prove that Fanorona is a draw. This means that if
both players are playing optimally a draw is the
result of the game. So far the moves d3-e3A and f2-e3A have
been proven to be optimal to achieve the draw in the
initial position.
Key Publication
- Schadd, M.P.D., Winands, M.H.M., Uiterwijk, J.W.H.M., Herik, H.J. van den, and Bergsma M.H.J. (2008). Best Play in Fanorona Leads to Draw. New Mathematics and Natural Computation, Vol. 4, No. 3, pp. 369-387.
