Signals

Wavelet representations of biomedical signals

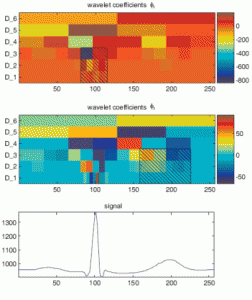
Design of an optimal wavelet for a ECG signal from: Karel J.M.H., Peeters R.L.M., Westra R.L., S.A.P. Haddad and W.A. Serdijn, Multiwavelet Design for Cardiac Signal Processing, 28th IEEE EMBS Annual International Conference, 2006

Current integrated light-weight and low-power sensor technology enable the high-resolution registration of various kinds of signals. These include biomedical relevant signals such as ECG, EEG, EMG, …, commonly denoted as EXG signals.

Our research in this area is focused, amongst others, on the analysis of biomedical systems and EXG signals in particular, with most notably aiming at detection and morphology. An example is the description of the morphology of the T-wave in ECG signals. Our approach consists of wavelet analysis of these signals, based on filterbanks employing (multi)wavelets that are optimized for the morphological characteristic of interest in the signal.

ECG inverse reconstruction of electrophysiological activity

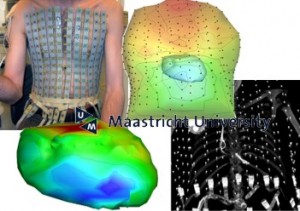
“Wavelet-sparsity based regularization over time in the inverse problem of electrocardiography”, M.J.M. Cluitmans, J.M.H. Karel, P.G.A. Volders, R.L. Westra, R.L.M. Peeters, EMBC 2013

The inverse problem of electrocardiography (ECGI) aims at reconstructing electrical heart-surface potentials from body-surface potentials. This problem is ill-posed, meaning that little variation in the starting data, for example due to measurement noise, yields enormous variations and erroneous reconstructions. In this research topic, we aim at obtaining regularized and validated solutions in human applications.

Current research focusses on involving physiological characteristics and wavelet sparsity in order to regularize the reconstruction.

The research is conducted in close cooperation with the department of cardiology of MUMC+.

Time frequency representations and causality analysis

Does a time series measures on the epicardium exhibit a causal relationship with a simultaniously measured time series on the endocardium? Is a signal in a certain region in the brain the concequence of a signal in a different regin? Is this relationship within a frequency band or between different frequency bands? What is the relative change in frequency in a signal after a stimulus?

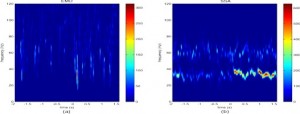
EMD vs SSD time frequency representation
“Singular spectrum analysis improves analysis of local field potentials from macaque V1 in active fixation task”, P. Bonizzi, J.M.H. Karel, P. De Weerd, E. Lowet, M. Roberts, R.L. Westra, O. Meste, R.L.M. Peeters, EMBC 2012

To answer these questions research is done in:

• Causal coupling analysis between time series
• Time-frequency decomposition of nonstationary and nonlinear time series
• Time-frequency analysis of multivariate time series

Techniques of interest here are Empirical Mode Decomposition and the Hilbert-Huang transform, Singular Spectral Analysis (SSA) and Multivariate EMD.

These techniques are applied in cooperation with various partners and with help of graduate students during internships.